The Dynamic Integrated model of Climate and the Economy (DICE)
Short overview
DICE is a global integrated assessment model developed by Nordhaus (1992) that represents the economic, policy and scientific aspects of climate change. It integrates the climate system in the framework of economic growth theory. In this approach, society invests in capital goods, thereby reducing consumption today, in order to increase consumption in the future. Investing in emissions reduction reduces consumption today but also prevents damage from climate change and increases consumption possibilities in the future. The DICE model has been used and developed by researchers outside the consortium.
The following figure shows a schematic flow chart of the major modules and logical structure of the model. The economy module includes the factors that are driving the economic growth (labour, population, capital and technology) and also the emissions of GHGs. The DICE model includes also several geophysical relationships that link the economy with the different forces affecting climate change. These relationships include the carbon cycle, a radiative forcing equation, climate-change equations and a climate-damage relationship. A key feature of IAMs is that the modules operate in an integrated fashion rather than taking variables as exogenous inputs from other models or assumptions. Therefore, the damage of climate change affects the production/output via a damage function.
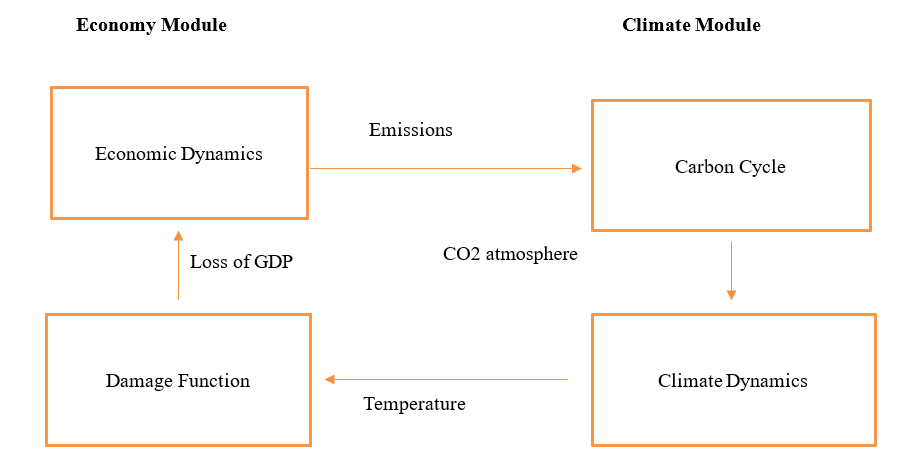
Structure of the DICE model
Technical specifications
In this section we include technical information on DICE extracted from Gonzalez-Eguino et al. (2016). More information can be found in Nordhaus and Sztorc (2013).
The model optimises a social welfare function, W, which is the discounted sum of the population-weighted utility of per capita consumption.
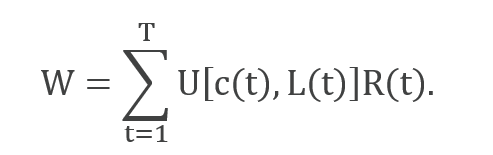
In this function, c(t) is the per capita consumption, L(t) is the population, and R(t) = (1 + ρ)-t is the discount factor of utility or welfare. ρ is the pure rate of social time preference or generational discount rate. The utility function is a constant elasticity function with respect to consumption of the form U(c) = c1-α /(1 − α). The parameter α is interpreted here as the generational inequality aversion.
Net output, Q(t), is the gross output, Y(t), reduced by damage, Ω(t), and mitigation costs, Λ(t). This net output, a function of capital, labour and technology that explains economic growth, can be devoted to consumption, C(t), and investment, I(t). Labour is proportional to population, while capital accumulates according to an endogenous savings rate.
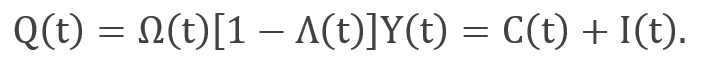
Damage from climate change, which is subject to large uncertainties, is represented in the DICE model by a quadratic function of globally averaged temperature change (TAT). The damage function is defined as Ω(t) = D(t)/[1+D(t)], where
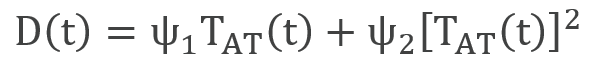
The abatement cost is a function of the emissions reduction rate, μ(t), and is estimated to be highly convex, indicating that the marginal cost of reductions rises from zero more than linearly with the reduction rate:
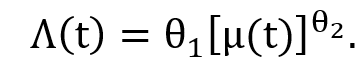
Total emissions,E(t), are fossil fuel and industrial emissions plus land-use change emissions, ELAND(t), and permafrost emissions, EPER(t). Fossil fuel and industrial CO2 emissions are determined by the level of carbon intensity, σ(t), times gross output, and reduced by the emissions reduction rate, μ(t). The only type of emissions subject to (endogenous) control in the DICE model is fossil fuel and industrial CO2.
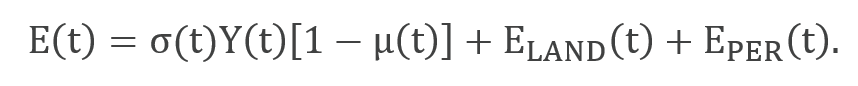
The geophysical equations link the GHG emissions to the carbon cycle, radiative forcing and temperature change. These equations are calibrated for the 21st century to large models or model experiments and have been updated (version 2013R) in line with AR5 of the IPCC (for example, in the current version, the equilibrium climate sensitivity has been reduced from 3 to 2.9). The following equation represents the equations of the carbon cycle for three reservoirs (j = AT, UP, and LO): atmosphere, upper oceans and biosphere, and lower oceans. All emissions flow into the atmosphere and the parameters φij represent the flow of carbon between reservoirs per period.
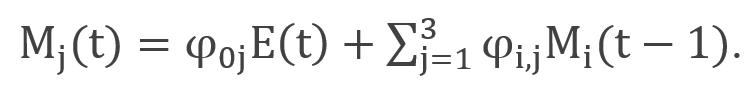
Finally, the relationship between CO2 concentrations and increased radiative forcing is given by:
F(t) = η{log2[MAT(t)/MAT(1750)]}+FEX(t)
where F(t) is the change in total radiative forcing of greenhouse gases from anthropogenic sources and FEX(t) is an exogenous forcing (which includes non-CO2 emissions and aerosols). For simplicity and transparency, we keep all aspects of the original DICE model unaltered. In this way, our results can easily be compared to previous findings obtained with the same model.
Regional, sectoral and GHG coverage
DICE is a global model. Therefore, it is not disaggregated between sectors, technologies or regions. The model includes CO,2 emissions from fossil fuel combustion endogenously and CO2 from other sources exogenously. Non-CO2 emissions are included aggregated as exogenous radiative forcing.
Recent use cases and limitations
DICE has been helpful in illustrating the economic cost and damage from climate action under different circumstances (Nordhaus, 2014; Moore and Diaz, 2015; Butler et al., 2014; or González-Eguino, 2016) However, different studies have shown that the results of the DICE model are very sensitive to the choice of the damage function (Pindyck, 2013), especially beyond 2°C. Therefore, some authors have used the DICE model using alternative damage functions (Ackerman et al., 2010 or Gonzalez-Eguino et al., 2017) and a sensitivity analysis of key parameters. Finally, the DICE model is an aggregated model that captures the economic cost of mitigation using only a cost function. Therefore, it cannot capture the complexity of the mitigation options of large-scale IAMs, such as, for example, the GCAM or TIAM models.
References
González-Eguino, M., & Neumann, M. B. (2016). Significant implications of permafrost thawing for climate change control. Climatic Change, 136(2), 381-388.
González‐Eguino, M., Neumann, M. B., Arto, I., Capellán‐Perez, I., & Faria, S. H. (2017). Mitigation implications of an ice‐free summer in the Arctic Ocean. Earth's Future, 5(1), 59-66.
Nordhaus, W.D., & Sztorc., P. (2013). DICE 2013R: Introduction and User’s Manual. Available at: http://www.econ.yale.edu/~nordhaus/homepage/documents/ DICE_Manual_103113r2.pdf.
Nordhaus, W. (2014). Estimates of the social cost of carbon: concepts and results from the DICE-2013R model and alternative approaches. Journal of the Association of Environmental and Resource Economists, 1(1/2), 273-312.
Moore, F. C., & Diaz, D. B. (2015). Temperature impacts on economic growth warrant stringent mitigation policy. Nature Climate Change, 5(2), 127.
Butler, M. P., Reed, P. M., Fisher-Vanden, K., Keller, K., & Wagener, T. (2014). Inaction and climate stabilization uncertainties lead to severe economic risks. Climatic change, 127(3-4), 463-474.

